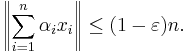B-convex space
In functional analysis, the class of B-convex spaces is a class of Banach space. The concept of B-convexity was defined and used to characterize Banach spaces that have the strong law of large numbers by Anatole Beck in 1962; accordingly, "B-convexity" is understood as an abbreviation of Beck convexity. Beck proved the following theorem: A Banach space is B-convex if and only if every sequence of independent, symmetric, uniformly bounded and Radon random variables in that space satisfies the strong law of large numbers.
Let X be a Banach space with norm || ||. X is said to be B-convex if for some ε > 0 and some natural number n, it holds true that whenever x1, ..., xn are elements of the closed unit ball of X, there is a choice of signs α1, ..., αn ∈ {−1, +1} such that
Later authors have shown that B-convexity is equivalent to a number of other important properties in the theory of Banach spaces. Being B-convex and having Rademacher type 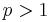 were shown to be equivalent Banach-space properties by Gilles Pisier.
were shown to be equivalent Banach-space properties by Gilles Pisier.
References
- Beck, Anatole (1962). "A convexity condition in Banach spaces and the strong law of large numbers". Proc. Amer. Math. Soc. 13 (2): 329–334. doi:10.1090/S0002-9939-1962-0133857-9. ISSN 0002-9939. MR0133857.
- Ledoux, Michel; Talagrand, Michel (1991). Probability in Banach spaces. Berlin: Springer-Verlag. pp. xii+480. ISBN 3-540-52013-9. MR1102015. (See chapter 9)